エイゾーだす。
前回、調子に乗って「自分で構図から考えて描いてやんぜ!」と意気込み撃沈したわけですが、数ある原因の中から最も大きなものとして「物の奥行表現方法を知らない」をあげました。
箱って3次元のものですが、それを紙に描くということは2次元に落とし込んであげなくてはならないですよね。真上とか真横とかからならただの長方形だから描けるけど、斜めってなった瞬間難しくなるわけです。
んで、そういったものを描くための手法があるということなので、調べてみましたよと。
パースってなんぞや
正確には違うんだけど遠近法や透視図と言ったものを日本では「パース」と呼んでいるそうな。
その内容や意味についてはネットにわんさか情報があるので、あえてここで書きません。たいして意味が分かっていない素人が書かないほうがいいよね。うん。
んでぱらぱらーと調べてみて、エイゾー1つの結論を得ました。
”遠くのものは小さく、近くのものは大きく見える。”
え?それだけ??そうです。結局はそういうことだと感じたんです。はい。
3つの透視図法
さてさて直方体のような平行線があるようなものを立体的に描く方法として3つの透視図法があるそうな。実際描いてみたほうがわかるじゃろということでやってみましたよ。
以下、基本的に直方体・・・まあ箱ですね。きれいな形の箱を題材とします。
アイレベルと消失点
平行線とはどこまで行っても交わらない線ですが、奥に行くに従い2本の直線がすぼまっていくのを見ると、人はそれを平行だと思ってしまうのだとか。最終的に無限遠で交わると。
平行を交わらせる消失点
え!?平行線なのに交わるの??非ユークリッドの話なの??
・・・取り乱しました。

ここには左右それぞれ3本の直線を描きましたが、左は何か向こう側に向かって続くまっすぐな道に見えるけど、右はそうは見えない。というか奥行きを一切感じない。
そう、人は程よいバカなのさ。
この平行線が交わるとされる点を消失点と呼ぶと。ふむ。
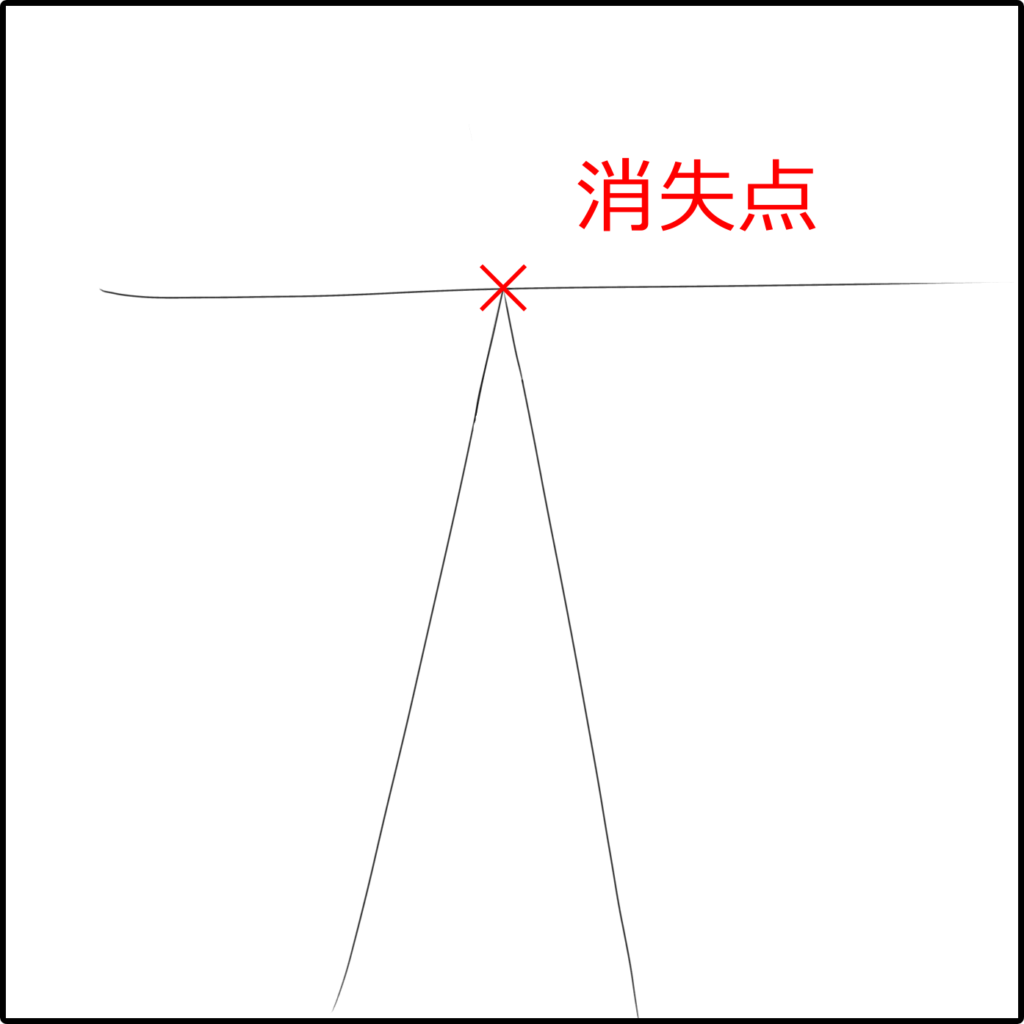
目線の高さも要素の一つ
絵を描くにあたって、3次元のものを2次元に表現するということは写真を撮るようなものですよね。
となるとカメラがあるし、カメラがあるということはカメラの位置もあるということです。
人がカメラを立って構えているか、座って構えているか、はたまた寝転んで構えているかでカメラの高さは変わりますよね。
カメラを地面と水平に構えていれば、カメラの高さのずっと先に地平線があります。
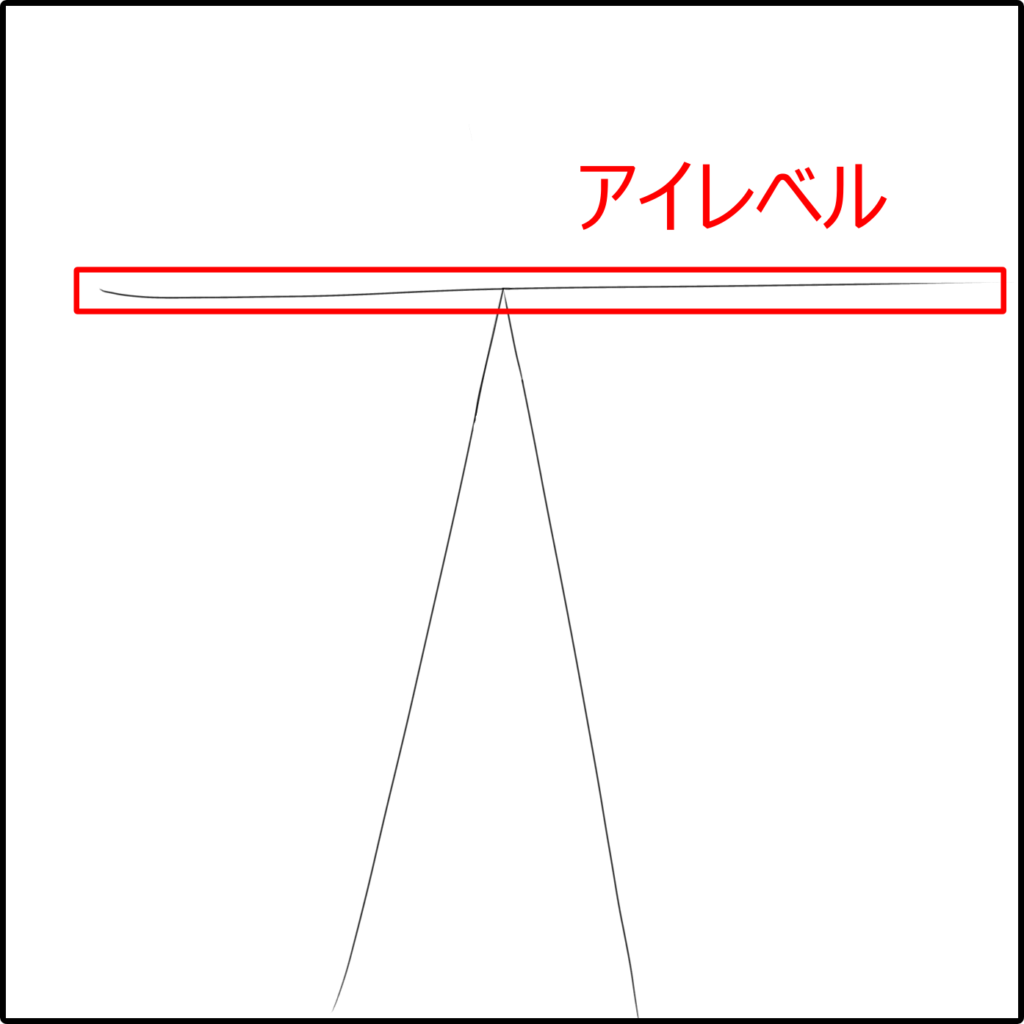
この地平線のことをアイレベルと呼ぶことが多いようです。
空を見上げて浮いている直方体を描く!なんてときは地平線ではないところにアイレベルが来るらしいので地平線=アイレベルというわけではないのですが、エイゾーはとりあえず地平線≒アイレベルとしておきます。
1点透視図法
箱の面の1つがこちらを向いている場合に使う手法だと。
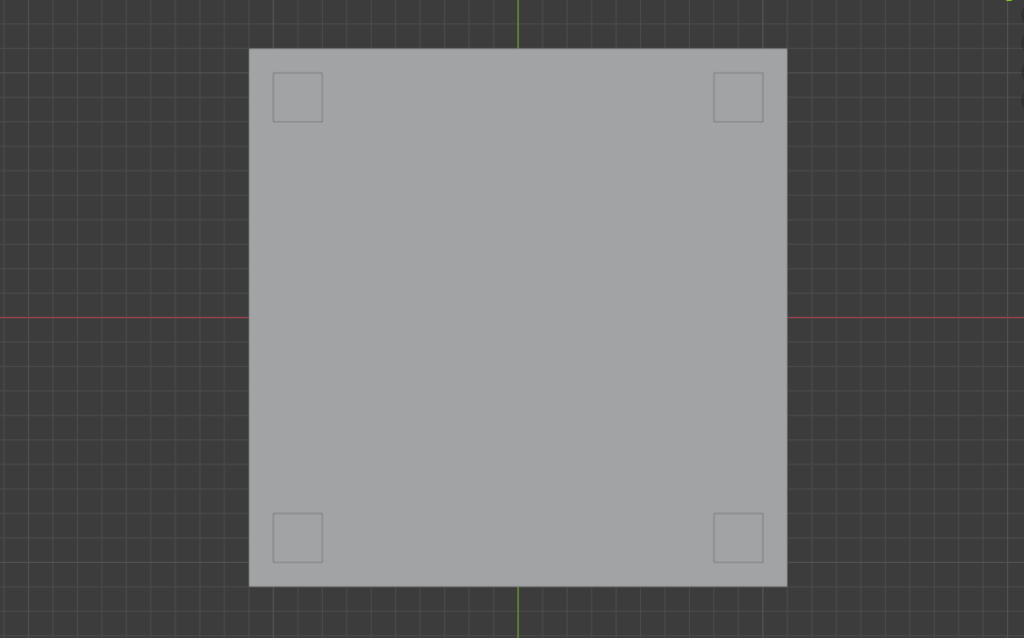
箱だとわかりずらいけど、例えば机とか。机を真下から見た時にきれいな長方形の頂点に脚があるとしますね。
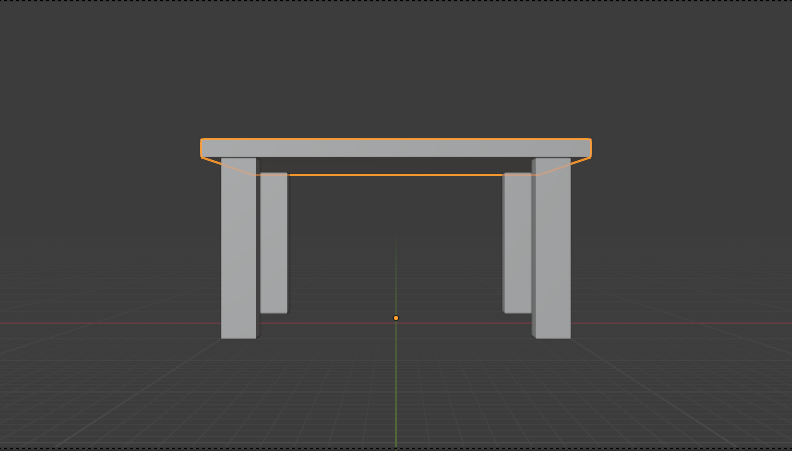
んで机を正面から見たら、本来なら奥の脚は手前の脚ですっぽり隠れるはずですよね。でも、実際は奥の脚が手前の脚よりやや内側に見える。つまり奥に行くにしたがってすぼまって見える。
これを違和感なく図にする手法がこの1点透視図法だと。ふむふむ。
すぼまっていくということはどこかでぶつかるということですよね。このぶつかる点を先に述べた消失点といって、この点はなんとアイレベル上にあるのだとか。
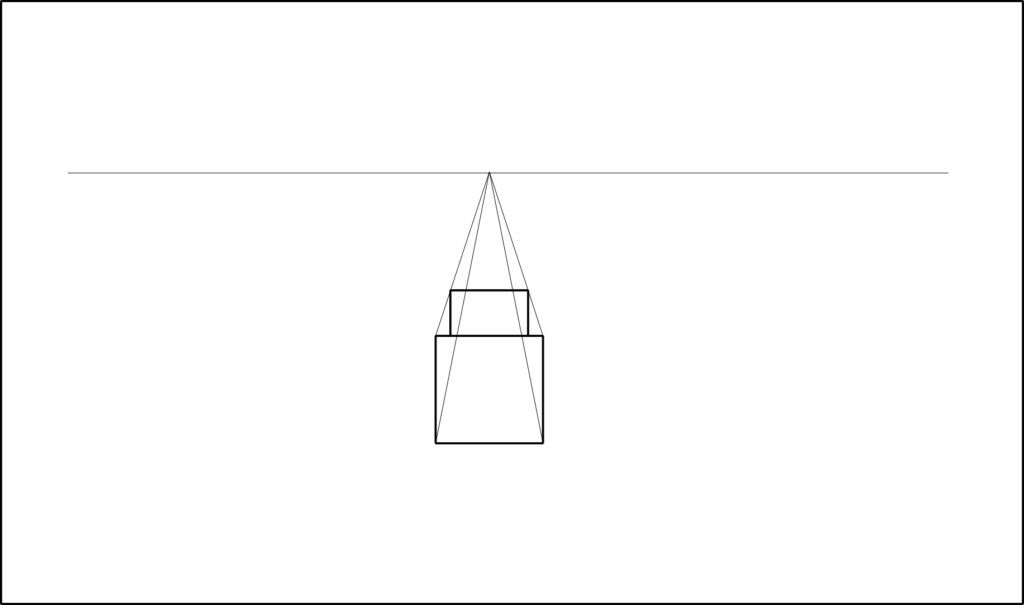
つまり地平線にて2つの平行線が交わるということですな。
2点透視図法
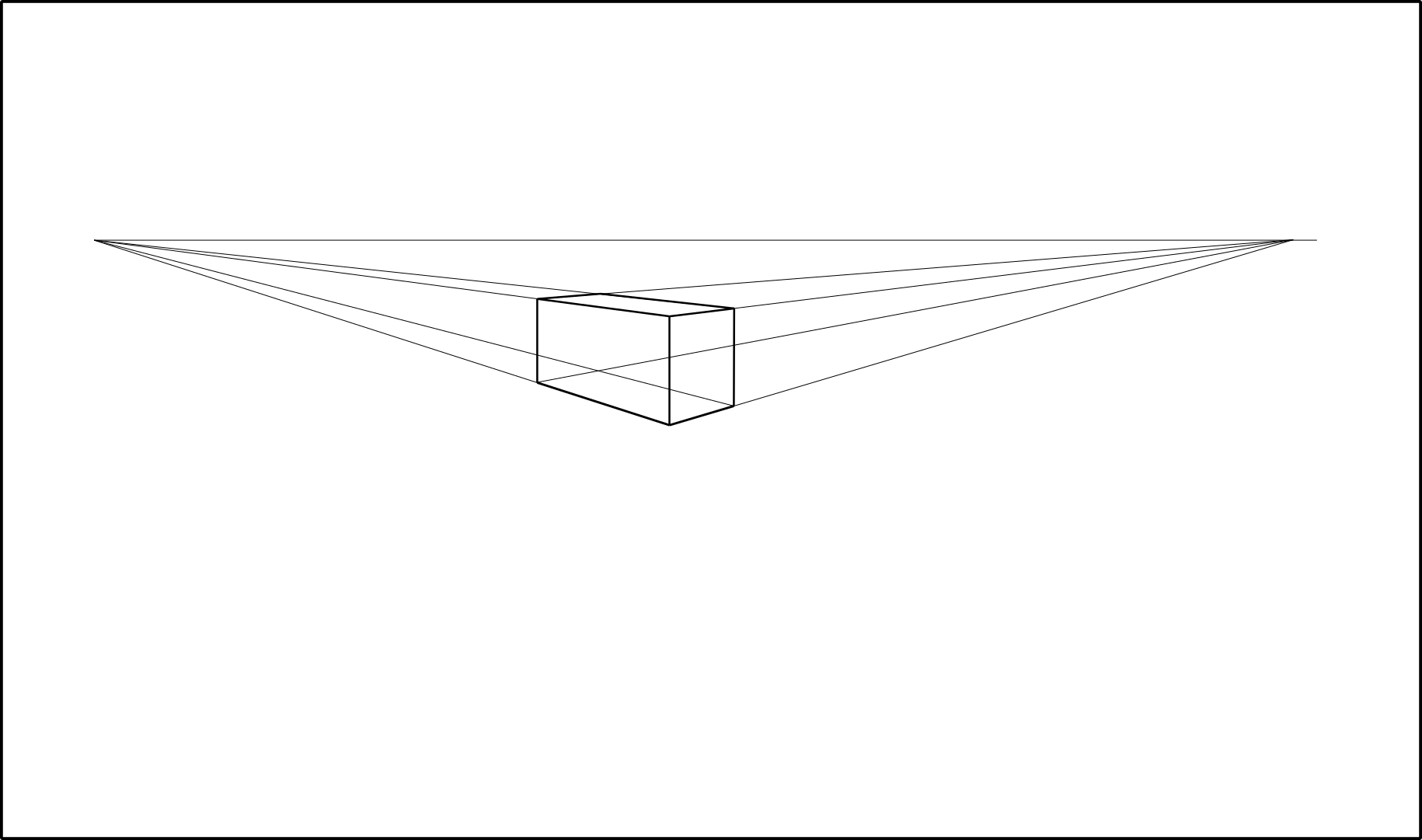
箱の面がこちらを向いていない場合は2点透視図法で描き表せると。
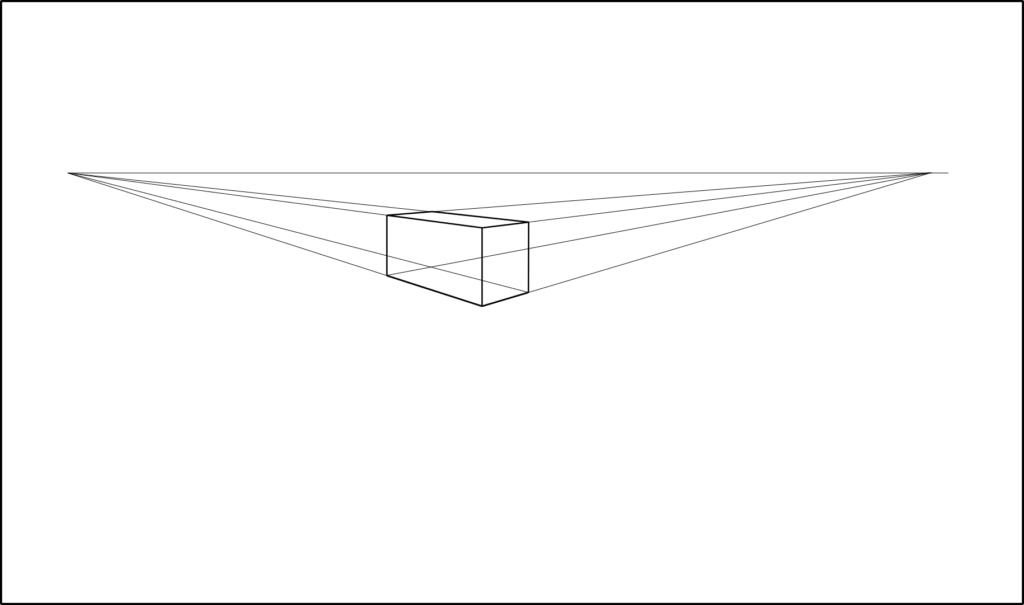
確かに向かって右の面も左の面も奥に向かっているわけなので、遠い方が小さく見えるという遠近法のもと、それぞれの平行線(横)は奥に向かってすぼまる必要があるんですな。ふむ。
この場合、消失点は2つできるんだけど、なんとどちらの消失点もアイレベル上に来るんだと。すげーな。え?すごくない??
3点透視図法
箱の面がこちらを向いておらず、かつ高いところから見下ろしていたりしたから見上げたりした状態を描くには3点透視図法を使うと。
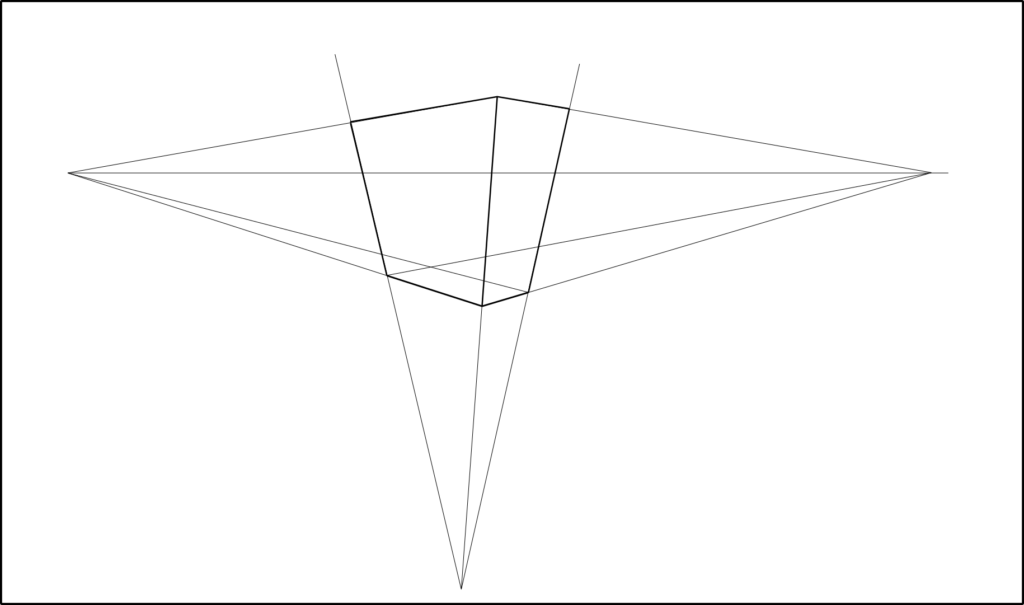
見上げていたとしたら、てっぺんは遠くなるもんね。ってことはてっぺんに向かってすぼまっていくわけだ。そちらにも消失点ができるというわけだね。
この3つ目の消失点は当然ながらアイレベル上にはないと。ふむ。
透視図法のなぞ
透視図法についてとりあえずどんなものかの大枠はわかったと思う。
ただ、よくわからんこともある。あるんだよ。
1点透視図法のX軸
1点透視図法は直方体の1つの面がこちらに正対していればよいと。こちら、つまり画面=キャンバスと直方体の1つの面が平行ならよいと。
こんなのでも1点透視図法でOKということ。
でも遠ければ小さいというのは横方向には適用されないの??正面にある物より横にある物の方が遠いと思うんだけどそこは関係ないのかいね??
1点透視図法なの?2点透視図法なの?
さっきの続きでこんな状態の場合、もはやこれは面がこちらを向いているとは言えないのでは・・・。
これは1点で描くのか2点で描くのかどっちなんだい・・・。
2点透視図法の消失点
消失点の設定の仕方が曖昧な紹介が多い気がするのよ。

この段階ではまだ消失点はない。だって奥行きがないのだから。
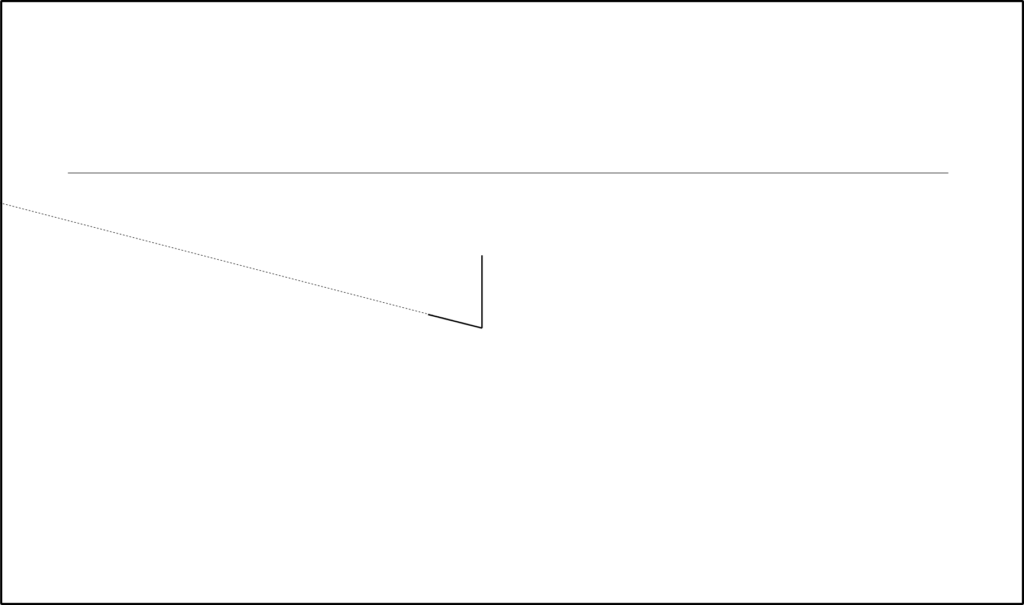
ここでまず一つ目の消失点が決まる。よね??画面の外だけど。
でもね同時に2つ目の消失点が決まっているはずなんだよ。だって箱(=直方体)の角は全部直角だからね。
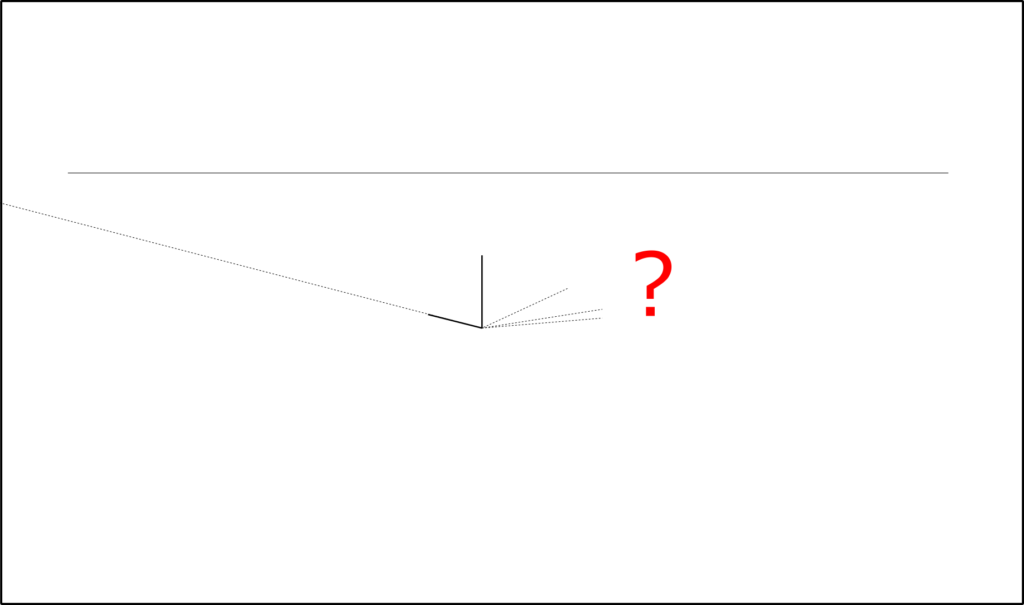
2点透視図法の説明をしているサイトはいっぱいあるけど、不自然に見えるものも多い気がするんだよなー。なんか歪んでるような。明らかに手前の角鋭角っすよね、っていうやつ。
一応導き出せるらしい
一応その2点目の消失点を導き出す計算というか方法はあるみたい。でもそのためにはカメラを構えている人がどこに立っているかを設定しなければならないみたい。
当然画面=キャンバスよりも手前に立っているわけで、紙の上に描きようがない。むむむ。
素人の結論
そう、だから結論は
”遠くのものは小さく、近くのものは大きく見える。”
これだけになっちゃう。
この透視図法という手法は正確な図を描くには必要なのかもしれないけれども、エイゾー毎回こんなんやりたくないっす。
数学は好きだし感覚より理詰めの方がありがたいんだけど、楽しく描けないよね。作図問題かって感じ。
ただ奥行きを表現する手法の1つとして、遠くのものは小さく、近くのものは大きく見えるということを再認識したというのが今回の収穫。そして奥行きのみがその歪みの影響を受けると。
ただ今回調べていてエイゾーに合ってそうな練習法を見つけたので、次回はそれに挑戦してみようと思います。
コメント